Limits
Limits are an essential part of calculus. Many students are intimidated by limits at first, but with just a few simple tips, you can become a pro at interpreting limits. In order to understand calculus, you must first understand what a limit is. A limit is the value a function approaches as the variable within that function gets nearer to a given value. Think of it this way: if x is very close to a certain number, what is f(x) close to? This section will cover the basic concepts of limits.
In calculus and precalculus,you will learn about right hand, left hand, and just normal limits. A right hand limit is represented by lim x--> 1+ f(x). This notation with a "+" sign after the approached value signifies that the question is asking for the value that f(x) is approaching coming from the right side of the function (in this case approaching x=1 from the right hand side).
Left hand limits have the same general idea as right hand limits except the "+" sign after the value x approaches is now a "-" sign. For example: lim x--> 1- f(x)
Regular limits just approach a given number with no specification of which side to approach from. This means that for the limit to exist, both the left hand and right hand limits of that given number must be equal to each other for a limit to exist. There are various reasons as to why the limit would not exist such as infinite discontinuity or jump discontinuity. In other words, the function is a piecewise function where the endpoints do not meet, or the function has a vertical asymptote at that value.
Some may get confused and think that if there is point discontinuity the limit does not exist at the hole in the graph, however this is incorrect. The existence of a limit NEVER depends on how the function may or may not be defined at a certain x value. In other words, we don't care if the function is continuous or not, as long as the left hand and right hand limits approach the same value, the limit exists!
Sometimes you will be given a limit and just plugging in the approached value will leave you in indeterminate form. When this occurs, you must try to manipulate the given equation into a simpler form where you get a real output value. There are multiple methods of doing this, it just depends on the problem. For example, you may try to factor the numerator and cancel out one part with the denominator to give you a simpler equation. In some instances where you may seem stuck, multiplying by the conjugate can be helpful.
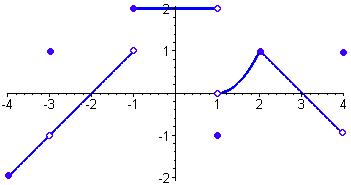
The above graph is a piecewise function with examples of jump and removable (point) discontinuity in multiple locations. Lets do some limit practice!
lim x-->-3=-1 (don"t let the removable discontinuity confuse you)
lim x-->-1+=2
lim x-->1= DNE
lim x-->4-= -1